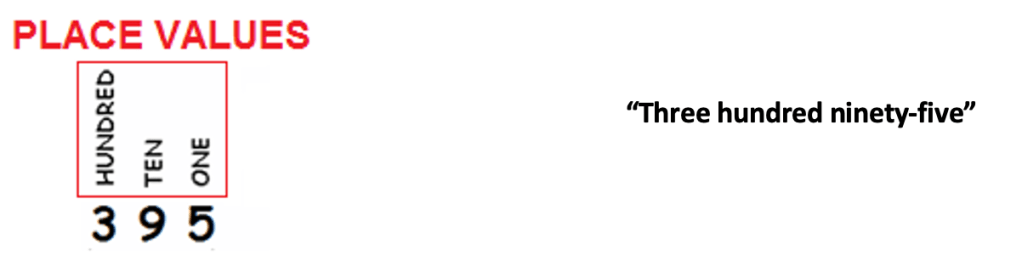Reference: The Book of Subject Clearing
Pre-Kindergarten
Lesson 1: ORIENTATION & SPATIAL SENSE
Lesson 2: QUANTITY & NUMBER SENSE
Lesson 3: PATTERNS & RELATIONAL SENSE
.
Kindergarten
Lesson 1: Orientation & Spatial Sense
Lesson 2: Numbers & Place Values
Lesson 3: Units & Fractions
Lesson 4: Counting & Measurements
Lesson 5: Numbers & Operations
Lesson 6: Patterns & Relational Sense
Lesson 7: Data Analysis & Probability
.
Primary School
Lesson 1: Numbers
Exercise: Reading Numbers from Dubb
Exercise: Writing Numbers from Dubb
Lesson 2: Addition
Exercise: Addition Problems from Dubb
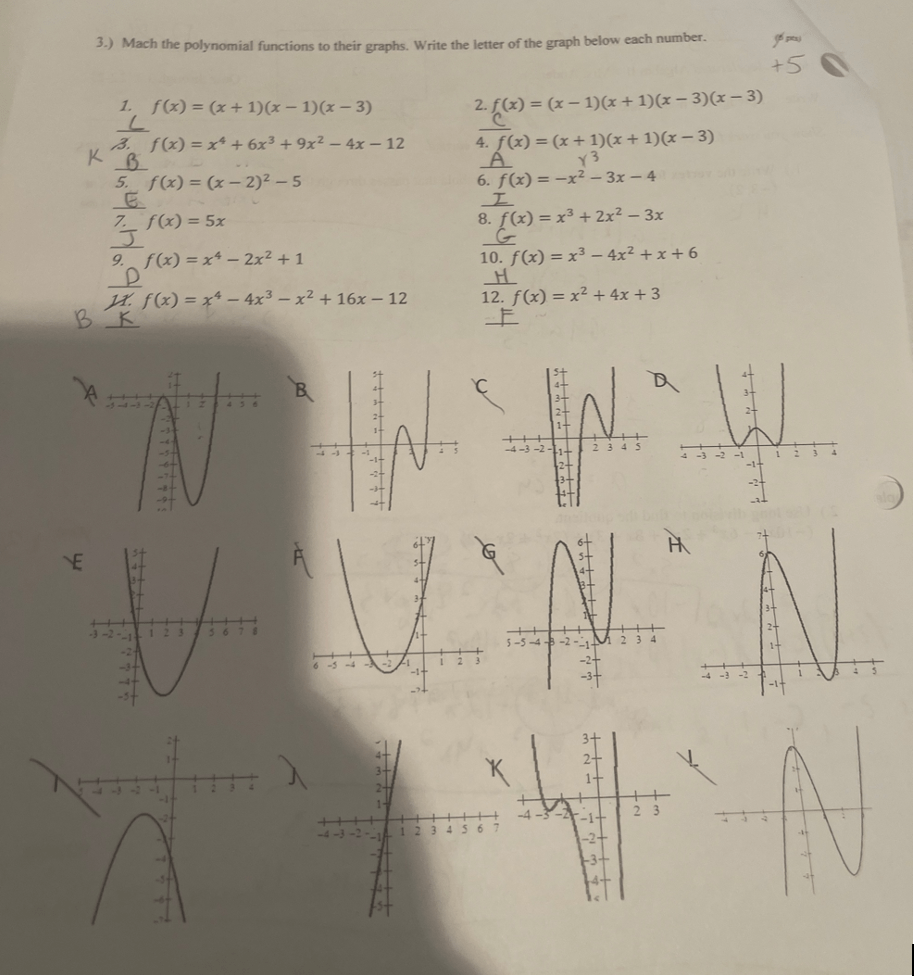
Lesson 3: Multiplication
Exercise: Multiplication Problems from Dubb
Lesson 4: Subtraction
Exercise: Subtraction Problems from Dubb
Exercise: Integer Problems from Dubb
Lesson 5: Division
Exercise: Short Division Problems from Dubb
Exercise: Long Division Problems from Dubb
Exercise: Arithmetic Expression Problems from Dubbs
Lesson 6: Units
Table: The Units of Measure
Exercise: Problems on Units from Dubb
- Long Measure
- Square Measure
- Rectangles
- Cubic Measure
- Time Measure
- Miscellaneous Tables
- Promiscous Examples
- Addition of Compound Numbers
- Subtraction of Compound Numbers
- Time between two Dates
- Time in Days between Two Dates
- Multiplication of Compound Numbers
- Division of Compound Numbers
.
Middle School
Introduction
- What is Mathematics?
- Mathematics Overview
- Counting and Abacus
- The Concept of Numbers
- Math Diagnostics
Lesson 1: Number to Integer
Exercise: Problems from Dubb (Word problems)
Lesson 2: Terms & Expression
Exercise: Problems from Dubbs (Word problems)
Lesson 3: Factoring
Exercise: Factoring Problems from Dubb
Lesson 4: Fractions
Exercise: Fraction Problems from Dubb
- Integer to Fraction
- Mixed Number to Improper Fraction
- Improper Fraction to Mixed number
- Reducing Fraction to a Denominator
- Reducing Fraction to Lowest Terms
- Reducing Fraction to LCM & GCD
- Addition of Fractions
- Subtraction of Fractions
- Multiplication of Fractions
- Multiplication Word Problems
- Division of Fractions
- Finding Part of a Number
- Reducing Complex Fractions
- Complex Fraction Word Problems
- Word Problems for Fractions
Lesson 5: Decimals
Exercise: Decimal Problems from Dubb
- Writing Decimals
- Reading Decimals
- Decimals to Common Fractions
- Common Fractions to Decimals
- Addition of Decimals
- Subtraction of Decimals
- Multiplication of Decimals
- Division of Decimals
Lesson 6: Review of Basics
Make yourself familiar with these basics
.
Further References
.