Category Archives: Quantum

Physics II: Chapter 17

December 27, 2023 – 9:16 AM

Reference: Beginning Physics II

Chapter 17: PARTICLES OF LIGHT AND WAVES OF MATTER

.

KEY WORD LIST

Localization, Interference, Energy Flow, Quantization, Light, Black Body Radiation, Photo-Electric Effect, Production of X-rays, Compton Scattering, Matter Waves, Probability Distribution, Maxwell’s Wave Equation, Schrödinger’s Equation, Dirac’s Equation, Wave Function, ­­­­Wave Packet, Uncertainty Principle, Zero Point Energy, Tunnelling.

(From KHTK) Particle, Quantum, Motion.

.

GLOSSARY

For details on the following concepts, please consult Chapter 17.

LOCALIZATION
A particle is defined as a “point”. The properties of velocity and acceleration are attributed to the whole particle. There is certainly no possibility of considering any one particle as being simultaneously at many different positions in space. A wave is defined as a disturbance that is spread over a fairly sizable area. A pure sinusoidal wave is spread out from plus to minus infinity. A pulse wave has a definite extent in space at any instance. One generally thinks of a wave as being a disturbance located simultaneously at many points of space. Therefore, the particle and wave picture differ on the question of localization.

INTERFERENCE
The interference or diffraction phenomenon is observed with waves but not with particles.

ENERGY FLOW
Both waves and particles carry energy and momentum. But there is a big difference in the mechanism of that energy flow. A wave carries this energy in a continuous fashion without discontinuous jumps in energy flow, even if the energy is greatly decreased. However, in case of particles, the energy comes in discontinuous pulses, with each pulse bringing a discrete amount of energy. The flow of energy is not uniform or continuous. This difference leads to the idea of quantization.

QUANTIZATION
In case of light, a continuously flowing wave seems to transport quantized units of energy.

LIGHT
Although the experiments on interference show that light behaves as a wave, the photo-electric effect provides the most convincing evidence that light must be considered to consist of particles. This apparent anomaly between wave and particle nature is resolved in the definitions from KHTK provided below.

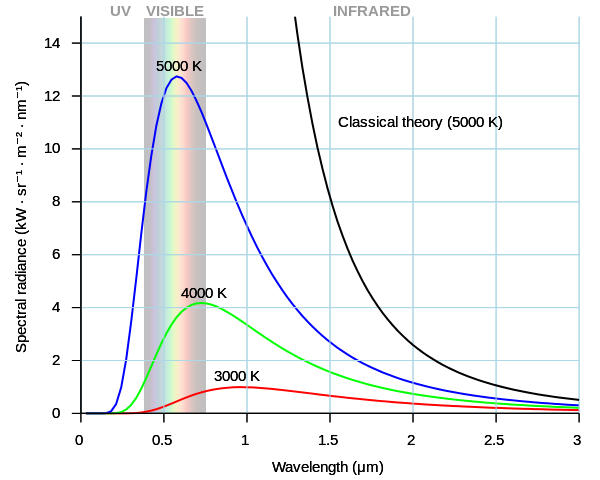
BLACK BODY RADIATION
This radiation is emitted over a continuous spectrum of frequencies. It increases rapidly at lower frequencies reaching a maximum and then starts to decline. Maxwell equations explain the distribution only at lower frequencies when it is increasing rapidly. They are unable to explain the rest of the distribution. But the whole distribution can be explained when energy is seen to be radiating in quanta that are proportional to frequency.

PHOTO-ELECTRIC EFFECT
In the photo-electric effect, a beam of light is shone on a metal, with the result that electrons are emitted from the metal. However, the maximum kinetic energy of the electrons emitted is found to depend on the frequency of the incident light and not on its intensity. This means that light energy has to be absorbed in quanta in the interaction that frees the electrons.

PRODUCTION OF X-RAYS
X-rays can be produced by taking energetic electrons and letting them strike a metal plate. When these electrons stop in the metal, they emit electromagnetic radiation over a large range of wavelengths.  The surprising experimental fact is that there is a minimum wavelength that can be emitted for each V (energy of the electrons). This minimum wavelength varies inversely with V but is not affected by the electron current density. These results cannot be explained by a wave theory of light.

COMPTON SCATTERING
The X-ray beam, after it is scattered by electrons, suffers a definite reduction in frequency. Compton showed that energy of the photon, as given by its frequency, is reduced by the same amount that the kinetic energy of the recoil electron is increased. Thus, the photon is a momentum carrying corpuscle that can transfer its momentum in a given direction to the atom. The Compton effect also implies that the electron must be treated as a wave and not as a particle.

MATTER WAVES
To conform with the case of electromagnetic waves, De Broglie hypothesized that the frequency and wavelength for electrons should be determined by the same basic relations used for photons. If De Broglie’s hypothesis is true, then the electrons represented by these waves should exhibit interference and diffraction appropriate to the wavelengths associated with the electron. When experiments were performed using crystals as diffraction gratings, this diffraction was indeed seen. Similar predictions for the wavelengths of more massive particles, such as protons and neutrons, have also been experimentally verified. Thus, at small scales, there is dualism in nature between waves and particles. The velocity of the particles is equal to the group velocity of its associated wave. Planck showed that energy is connected to frequency, E = hf. De Broglie then showed that momentum is connected to wavelength, p = h/λ. This is a fundamental relation of the Quantum Theory.

PROBABILITY DISTRIBUTION
The interference of waves in the double slit experiment creates a distribution of the intensity of light. Quantum mechanics interprets this as a probability distribution of “point” particles called photons. This concept, that the only thing that we can predict is the probability of a photon’s location, is a basic concept of quantum mechanics.

MAXWELL’S WAVE EQUATION
Thus in the case of a photon, Maxwell’s wave equation gives the probability amplitude for finding a photon. This equation has to be solved to predict the behavior of the photon.

SCHRÖDINGER’S EQUATION
This is a similar equation that provides the probability amplitude for finding a non-relativistic electron.

DIRAC’S EQUATION
This equation provides the probability amplitude for finding a relativistic electron.

WAVE FUNCTION
The central idea is that there is some wave equation which has to be solved to predict the behavior of a particle. When this equation is solved for a particular case, the resulting wave (called a wave function) gives an amplitude which, when squared, is proportional to the probability distribution of the particles.

­­­­WAVE PACKET
Pulses of waves can be obtained by superposing a large number of regular traveling waves of different wavelengths. Such a pulse is called a “wave packet.” Such a packet traveling through space indeed resembles a localized particle.

UNCERTAINTY PRINCIPLE
The uncertainty principle states that if one wants to describe a particle (at a given time) as being localized in a region ∆x (i.e. have a spatial uncertainty ∆x), then that particle must have an uncertainty in its x direction momentum, ∆p, which is at least as large as h/∆x. Similarly, if one wants the x direction momentum to be known to within ∆p, then there must be an uncertainty in the position of the particle which is at least as large as ∆x = h/∆p. Of course, if p is uncertain, so is v and the kinetic energy.

ZERO POINT ENERGY
This means that particles of matter, even if the temperature is at absolute zero where there is no thermal energy, must still have an average kinetic energy related to this range of momenta. This kinetic energy at a temperature of absolute zero, is called the “zero-point energy”, and there is no way to avoid having this minimum amount of energy.

TUNNELLING
Energy uncertainty of a particle allows it to surmount the barrier from the inside to the outside of the well for the short time needed to travel and escape from the well. This process is called tunneling, since the particle appears to have dug a hole through the wall of the well and emerged on the outside. This process actually occurs in the radioactive decay of nuclei.

.

The following definitions are from the philosophy of KHTK:

PARTICLE
A particle is not a “point,” but it has a volume that is filled with substance. The substance within a particle has uniform consistency throughout. The more condensed is the substance, the smaller is the size of the particle. This predicts the relative sizes of a proton and an electron in a hydrogen atom. The size of the electron is equivalent to the size of the hydrogen atom. On the other hand, the size of the proton is roughly 2000 times smaller because its substance is that much condensed. This provides a proper visualization of the hydrogen atom, where an extremely small proton exists at the center of the only electron there is. A very condensed particle, like proton, may appear to be spherical in shape; but as the consistency of substance decreases, as in the electron, the particle is likely to expand in size and flatten into the shape of a disk.

QUANTUM
This quantum is the amount of energy involved in the process of radiating and getting absorbed. It does not necessarily mean that this energy exists in space in a pulse form. In space it may simply appear as a certain consistency (a degree of condensation) of energy.

MOTION
When the difference in condensations is very large, the condensed substance may appear as a particle next to the uncondensed substance. But if the difference in condensation is comparable, the two substances may appear as waves when set next to each other. Therefore, ‘wave’ and ‘particle’ is a matter of looking at substance at different scale of condensation. If you greatly magnify a particle, you may see waves inside it as a disturbance. The wave inside a particle may have a ‘motion’ commensurate with the condensation of its substance. This may appear to give the particle its relative speed compared to another particle.

We find that a slight change in the condensation of substance creates a huge change in the relative speed of its particle. This may be the leverage that thought has over physical movement. All animation in the body is most likely produced by infinitesimal shifts in condensations of substance. This principle may also underlie in controlling the speed and direction of the UFOs. The change in condensation must apply equally to the occupants of the UFO for intense accelerations not to be felt by them.

.

By vinaire | Also posted in Physics | Comments (0)

The Quantum Phenomena (old)

January 26, 2018 – 11:16 PM
Quantum

Reference: Disturbance Theory

.

The electromagnetic cycles are packed so closely in the nucleus of an atom that they may be considered to be “collapsed”. By “collapsed” we mean that that the electromagnetic cycles have become infinitesimal and they cannot be distinguished one from another. Therefore, these cycles form a continuum within the nucleus.  This condition is identified as “mass”.

The Newtonian mechanics is applicable within the material domain where it treats space and time as absolute and independent of each other.  This is possible because the continuum of mass provides constancy to space and time. Thus, arbitrary material units may be used to measure the distance between two points, and the time interval between two events.

Underlying the material domain is the domain of electromagnetic field. In this domain the frequencies are smaller and the variations in them are depicted as a spectrum (see The Spectrum of Substance ). The cycles of these frequencies may be distinguished from one other and counted. In short, we do not have a continuum in the electromagnetic domain; and no constancy of space and time. The theory of relativity identifies this condition as “length contraction” and “time dilation” from the perspective of the material domain.

The quantum phenomenon arises in the electromagnetic domain due to the absence of continuum.

In the electromagnetic domain, length and time are determined by counting the number of cycles between two points. Thus, each electromagnetic cycle is a quantum entity, and length and time do not exist within the cycle.

The fundamental quantum entity is the electromagnetic cycle.

Since both length and time are “counted” by the number of cycles, they are not independent of each other. They are related by the universal constant “c” known as the speed of light.

This quantum characteristic of the electromagnetic cycle may also explain the phenomenon of quantum entanglement. At very low frequencies, one electromagnetic cycle may extend to hundreds of miles when it is superimposed on the material domain. Any action within the span of this cycle will appear as simultaneous and instantaneous from the perspective of material domain.

Quantum entanglement will then be a phenomenon that will occur at very low frequencies. The lower is the frequency the farther will the effects be observed.

.

By vinaire | Comments (1)

Newton, Einstein & Quantum Mechanics

January 22, 2018 – 8:26 AM
Newton-Einstein
Reference: Disturbance Theory

.

The scientific method represents only part of what defines scientific thinking. It covers the research into the physical aspects of the universe only. When it comes to researching both physical and mental aspects of the universe, it requires mindfulness. The criterion of mindfulness is the establishment of continuity, harmony and consistency in what is observed. This is the establishment of objectivity. The scientific method is a “sub set” of mindfulness.

The scientific method limits objectivity to physical phenomena. Mindfulness, as defined above, extends objectivity to all phenomena. This difference is clearly accentuated in how Einstein and Descartes looked at space. Einstein’s approach characterizes the scientific method, whereas, Descartes approach characterizes mindfulness. Please see, The Problem of “Empty Space”.

Einstein tried to address the mental aspects through his “thought experiments” but it fell short of mindfulness. Einstein did make great strides with his thought experiments but he failed to connect the finite speed of light with light having a finite amount of inertia. His theory of relativity addresses material systems only using light as a reference point of “zero” inertia. This approach works for material systems but fails for the atomic region for which the inertia of light cannot be ignored. The lack of understanding of the concept of inertia is the basis of the lack of unification among Newton, Einstein and Quantum mechanics. Please see, The Problem of Inertia.

Here is my take on gravitation from the viewpoint of mindfulness. A force exists in a field because of a frequency gradient. Electromagnetic forces exist due to frequency gradients in the lower gamma region, which is the region of electrons. Nuclear forces exist due to frequency gradients in the upper gamma region, which is the region of neutrons and protons. Thus, the nature of force depends on the area of the spectrum where the frequency gradient occurs. Please see, The Spectrum of Substance.

Matter approximates the very high frequency at the upper end of the electromagnetic spectrum, and space approximates the very low frequency at the bottom. The frequency gradient stretches with distance in space, and this appears as the force of gravitation.

The above explanation follows from a classical reasoning. In this approach mass comes about due to the collapse of very high frequencies in the nucleus of the atom. This represents the gradient at the upper end of the electromagnetic spectrum.

The above reasoning also explains space as a very low frequency electromagnetic field that dilutes the overall frequency gradient, which expresses itself as gravitational force.

The Higgs Mechanism is a product of a mathematical approach that lacks an underlying physical theory.

.

By vinaire | Comments (4)

Classical to Quantum Mechanics

November 13, 2017 – 7:44 AM
Blackbody Radiation
Reference: Disturbance Theory

.

  1. The Classical Mechanics made a transition into Quantum Mechanics at the beginning of 20th century when the interactions between field and matter were studied. The first field-matter interaction was encountered in the Black Body Radiation. The classical equipartition theory failed to account for the energy of the emitted electromagnetic spectrum.

  2. There was a thermodynamic equilibrium observed between the temperature of the body and the spectrum of the electromagnetic field surrounding the body. In other words, the agitation of atoms (temperature) was in equilibrium with the absorption and emission of thermal electromagnetic radiation (spectrum).

  3. The formulae based on classical thermodynamics could either explain the low frequency part of the spectrum (Raleigh-Jean formula), or the high frequency part of the spectrum (Wien’s Distribution formula), but not the entire spectrum at once. Planck found the formula, which could replicate the entire spectrum by ingeniously interpolating between the above two formulae. This was purely an empirical effort based on mathematics. He came up with the explanation for his formula later.

  4. From Derivation of Planck’s radiation law:

    In order to reproduce the formula which he had empirically derived and presented in October 1900, Planck found that he could only do so if he assumed that the radiation was produced by oscillating electrons, which he modelled as oscillating on a massless spring (so-called “harmonic oscillators”). The total energy at any given frequency would be given by the energy of a single oscillator at that frequency multiplied by the number of oscillators oscillating at that frequency.

    However, he had to assume that

    1. The energy of each oscillator was not related to either the square of the amplitude of oscillation or the square of the frequency of oscillation (as it would be in classical physics), but rather just to the frequency,
      E α ν
    2. The energy of each oscillator could only be a multiple of some fundamental “chunk” of radiation, hν, so En = nhν
      where n = 0, 1, 2, 3, 4
    3. The number of oscillators with each energy En was given by the Boltzmann distribution, so

      Nn = N0e–nhν/kT

      where N0 is the number of oscillators in the lowest energy state.

      By combining these assumptions, Planck was able in November 1900 to reproduce the exact equation which he had derived empirically in October 1900. In doing so he provided, for the first time, a physical explanation for the observed blackbody curve.

  5. The frequency of the radiation matched the frequency of the “oscillators” in the body. The high frequency oscillators could be activated only when energy proportional to their frequency was available. Therefore, lesser numbers of oscillators were activated at higher frequencies. Planck thus resolved the Ultraviolet catastrophe.

  6. We may postulate that the kinetic and potential states of oscillators produce the electric and magnetic states of radiation respectively. Therefore, the electric state may be related to magnetic state the way the kinetic state is related to potential state. The magnetic state could be a concentrated electric state; and the electric state could be a flowing magnetic state.

  7. Thus an electromagnetic cycle consists of a pulse of energy of magnitude ‘h’. A three-dimensional electromagnetic field is made up of such dynamic pulses.

.

By vinaire | Comments (1)

Black-body radiation (Notes)

November 13, 2017 – 6:35 AM
Black_body
Reference: Disturbance Theory

.

Black body

  1. A black body is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence.

  2. A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic radiation called black-body radiation.

  3. The radiation has a spectrum that is determined by the temperature alone, not by the body’s shape or composition.

  4. It is extremely difficult to realize a perfect black body, for which, the absorption of radiation is 100%. Transmission and reflection is zero.

.

Thermodynamic equilibrium

  1. In thermodynamic equilibrium all kinds of equilibrium hold at once.

  2. It is characterized by no net macroscopic flows of matter or of energy.

  3. Any microscopic exchanges are perfectly balanced.

  4. The temperature is spatially uniform.

  5. Entropy maximizes with equilibrium.

Thermodynamic state

  • A thermodynamic system is a macroscopic object, the microscopic details of which are not explicitly considered in its thermodynamic description.

Internal energy

  • It excludes the kinetic energy of motion of the system as a whole and the potential energy of the system as a whole due to external force fields.

Boltzmann constant

  • The Boltzmann constant (kB or k), which is named after Ludwig Boltzmann, is a physical constant relating the average kinetic energy of particles in a gas with the temperature of the gas. It is the gas constant R divided by the Avogadro constant NA.

.

Equipartition theorem

  1. It relates the temperature of a system to its average energies in thermal equilibrium.

  2. It assumes that energy is shared equally among all of its various modes. For example, the average kinetic energy per degree of freedom in translational motion of a molecule should equal that in rotational motion.

  3. It gives the average values of individual components of the energy, such as, the kinetic energy of a particular particle, or the potential energy of a single spring. For example, it predicts that every atom in a monatomic ideal gas has an average kinetic energy of (3/2) kBT in thermal equilibrium.

  4. When the thermal energy kBT is smaller than the quantum energy spacing in a particular degree of freedom (such as at lower temperatures), the average energy and heat capacity of this degree of freedom are less than the values predicted by equipartition.

  5. Such decreases in heat capacity were among the first signs to physicists of the 19th century that classical physics was incorrect and that a new, more subtle, scientific model was required.

  6. Along with other evidence, equipartition’s failure to model black-body radiation—also known as the ultraviolet catastrophe—led Max Planck to suggest that energy in the oscillators in an object, which emit light, were quantized, a revolutionary hypothesis that spurred the development of quantum mechanics and quantum field theory.

.

Rayleigh–Jeans law

  1. The Rayleigh–Jeans law revealed an important error in physics theory of the time.

  2. The law predicted an energy output that diverges towards infinity as wavelength approaches zero (as frequency tends to infinity).

  3. Measurements of the spectral emission of actual black bodies revealed that the emission agreed with the Rayleigh–Jeans law at low frequencies but diverged at high frequencies; reaching a maximum and then falling with frequency, so the total energy emitted is finite.

.

Ultraviolet catastrophe

  1. The ultraviolet catastrophe was the prediction of classical physics that an ideal black body at thermal equilibrium will emit more energy as the frequency increases.

  2. A blackbody would release an infinite amount of energy, contradicting the principles of conservation of energy.

  3. The ultraviolet catastrophe results from the equipartition theorem of classical statistical mechanics which states that all harmonic oscillator modes (degrees of freedom) of a system at equilibrium have an average energy of (1/2)kT. It assumes that vibrating modes can increase infinitely.

.

Black-body radiation

  1. Black-body radiation is the thermal electromagnetic radiation within or surrounding a body.

  2. It has a specific spectrum and intensity that depends only on the body’s temperature.

  3. As its temperature increases the peak of the spectrum shifts from infra-red toward higher frequencies of visible light.

  4. Black-body radiation has a characteristic, continuous frequency spectrum.

  5. If each Fourier mode of the equilibrium radiation in an otherwise empty cavity with perfectly reflective walls is considered as a degree of freedom capable of exchanging energy, then, according to the equipartition theorem of classical physics, there would be an equal amount of energy in each mode.

  6. Since there are an infinite number of modes this implies infinite heat capacity (infinite energy at any non-zero temperature), as well as an unphysical spectrum of emitted radiation that grows without bound with increasing frequency, a problem known as the ultraviolet catastrophe.

  7. Instead, in quantum theory the occupation numbers of the modes are quantized, cutting off the spectrum at high frequency in agreement with experimental observation and resolving the catastrophe. The study of the laws of black bodies and the failure of classical physics to describe them helped establish the foundations of quantum mechanics.

Explanation

  1. The radiation from matter represents a conversion of a body’s thermal energy into radiative energy. At thermal equilibrium, matter emits and absorbs radiative substance. The radiative substance has a characteristic frequency distribution that depends on the temperature only.

  2. At thermodynamic equilibrium the amount of every wavelength in every direction of radiative energy emitted by a body at temperature T is equal to the corresponding amount that the body absorbs because it is surrounded by light at temperature T.

  3. The black-body curve is characteristic of thermal light, which depends only on the temperature of the body. The principle of strict equality of emission and absorption is always upheld in a condition of thermodynamic equilibrium.

  4. By making changes to Wien’s radiation law consistent with thermodynamics and radiation, Planck found a mathematical expression fitting the experimental data satisfactorily. Planck had to assume that the energy of the oscillators in the cavity was quantized, i.e., it existed in integer multiples of some quantity.

  5. Einstein built on this idea and proposed the quantization of radiative energy itself in 1905 to explain the photoelectric effect.

  6. These theoretical advances eventually resulted in the superseding of classical electromagnetism by quantum electrodynamics. These quanta were called photons and the black-body cavity was thought of as containing a gas of photons.

  7. In addition, it led to the development of quantum probability distributions, called Fermi–Dirac statistics and Bose–Einstein statistics, each applicable to a different class of particles, fermions and bosons.

Also see: Classical to Quantum Mechanics

.

By vinaire | Comments (0)