Mathematics | Vinaire's Blog

Many hundreds of years ago in a small Italian town, a merchant had the misfortune of owing a large sum of money to the moneylender. The moneylender, who was old and ugly, fancied the merchant’s beautiful daughter so he proposed a bargain. He said he would forgo the merchant’s debt if he could marry the daughter. Both the merchant and his daughter were horrified by the proposal.

The moneylender told them that he would put a black pebble and a white pebble into an empty bag. The girl would then have to pick one pebble from the bag. If she picked the black pebble, she would become the moneylender’s wife and her father’s debt would be forgiven. If she picked the white pebble she need not marry him and her father’s debt would still be forgiven. But if she refused to pick a pebble, her father would be thrown into jail.

They were standing on a pebble strewn path in the merchant’s garden. As they talked, the moneylender bent over to pick up two pebbles. As he picked them up, the sharp-eyed girl noticed that he had picked up two black pebbles and put them into the bag. He then asked the girl to pick her pebble from the bag.

What would you have done if you were the girl? If you had to advise her, what would you have told her? Careful analysis would produce three possibilities:

1. The girl should refuse to take a pebble.
2. The girl should show that there were two black pebbles in the bag and expose the moneylender as a cheat.
3. The girl should pick a black pebble and sacrifice herself in order to save her father from his debt and imprisonment.

The above story is used with the hope that it will make us appreciate the difference between lateral and logical thinking.

The girl put her hand into the money bag and drew out a pebble. Without looking at it, she fumbled and let it fall onto the pebble-strewn path where it immediately became lost among all the other pebbles.*

“Oh! How clumsy of me,” she said. “But never mind, if you look into the bag for the one that is left, you will be able to tell which pebble I picked.” Since the remaining pebble is black, it must be assumed that she had picked the white one. And since the moneylender dared not admit his dishonesty, the girl changed what seemed an impossible situation into an advantageous one.

*MORAL OF THE STORY: Most complex problems do have a solution, sometimes we have to think about them in a different way.*

By vinaire | Comments (0)

Real Numbers

February 9, 2014 – 8:48 PM

Natural numbers are counting numbers. Counting refers to things. Counting starts from 1 and goes “one more” forever.

Whole numbers include the additional idea of “nothing” as the absolute reference point. This reference point exists at the beginning of the number line as zero (0). One may then count forever starting from 0. Thus, whole numbers include natural numbers.

Whole number = 0 + natural number (in absolute sense)

Integers include the idea of a relative reference point. This reference point may exist anywhere on the number line. This reference point is also called “zero”, and one counts from this point forever in either direction. Counting to the right is positive. Counting to the left is negative. Thus, integers include whole numbers.

Positive number = 0 + natural number (in relative sense)

Negative number = 0 – natural number (in relative sense)

Rational numbers fill the gaps between integers on the number line, such as, between 0 and 1, between 1 and 2, etc. These numbers are represented as a ratio of two integers, such as, “1/2”, “2/3”, “7/4”, etc. Rational numbers include all integers. Rational numbers may be represented by decimal numbers that either are recurring or terminate.

Rational number = ratio of two integers

Irrational numbers also fill the gaps between integers, but they cannot be represented as ratio of two integers. Example of irrational number is the “circumference to diameter ratio” of a circle. This is known as “π (pi)”. Other examples are square roots of prime numbers, such as, √2, √3, etc. Irrational numbers may be approximated by decimal numbers of any length.

All the above numbers together make up the set of Real Numbers. The squares of real numbers are always positive and never negative. The square roots of negative numbers are represented by Imaginary numbers.

By vinaire | Comments (8)

Shorthands for Counting

January 26, 2014 – 7:20 AM

Addition = Counting together

Multiplication = Repeated addition

Exponentiation = Repeated Multiplication

Subtraction = Opposite of addition

Division = Opposite of multiplication

By vinaire | Comments (2)

The Commutative Property

January 25, 2014 – 11:06 PM

The Commutative Property applies to addition as follows:

5 + 3 = 0 + 5 + 3 = 0 + 3 + 5 = 3 + 5

Note that 0 (zero) is the neutral element for addition. The operation of plus appears for 5 when 0 is placed in front of it. It does not change the meaning. The commutative property is applied by rearranging the number with its operation. We note that plus for addition is also omitted when 0 is omitted.

3 = 0 + 3

The Commutative Property applies to subtraction as follows:

5 – 3 = 0 + 5 – 3 = 0 – 3 + 5 = – 3 + 5

Note that 0 (zero) is the neutral element for subtraction as well, because addition and subtraction are opposite of each other. The commutative property is applied by rearranging the number with its operation. Therefore, 3 is moved with its minus operation. When 0 is removed, the ‘minus’ becomes a ‘negative’ sign.

– 3 = 0 – 3

The Commutative Property applies to multiplication as follows:

6 x 2 = 1 x 6 x 2 = 1 x 2 x 6 = 2 x 6

Note that 1 (one) is the neutral element for multiplication. The operation of multiplication appears for 6 when 1 is placed in front of it. It does not change the meaning. The commutative property is applied by rearranging the number with its operation. We note that multiplication sign is also omitted when 1 is omitted.

2 = 1 x 2

The Commutative Property applies to division as follows:

6 ÷ 2 = 1 x 6 ÷ 2 = 1 ÷ 2 x 6 = 1/2 x 6

Note that 1 (one) is the neutral element for division as well, because multiplication and division are opposite of each other. The commutative property is applied by rearranging the number with its operation. Therefore, 2 is moved with its division operation. 1 divided by 2 becomes the fraction half.

1 ÷ 2 = 1/2 (half)

By vinaire | Comments (5)

Vinaire's Blog

Category Archives: Mathematics

Elementary School Math Review

COUNTING REVIEW

Reference: MILESTONE 1: Numbers & Place Values

Review 01: Counting on Fingers

Review 02: Counting on Abacus

Review 03: Counting with Regrouping

Review 04: Writing the Count

Review 05: Counting to One Hundred

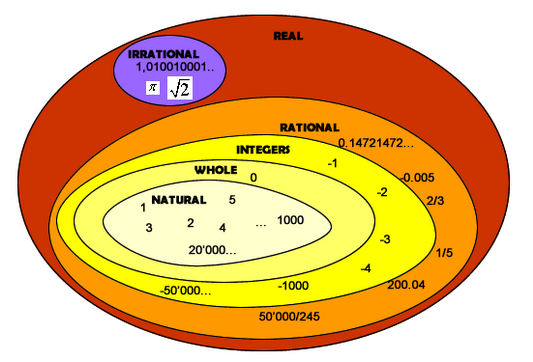
Review 06: Units and Numbers

Review 07: Numbers and Digits

Review 08: Place Values

ADDITION REVIEW

Reference: MILESTONE 2: Addition

Review 10: Addition is Counting Together

Review 11: Adding by Counting More

Review 12: Adding by Regrouping

Review 13: Adding Double-Digit Numbers

Review 14: Practice Mental Addition

Review 15: Adding by Columns

SUBTRACTION REVIEW

Reference: MILESTONE 3: Subtraction

Review 20: Subtraction is Finding the Difference

Review 21: Subtracting by “Reverse Addition”

Review 22: Subtracting by Columns (Traditional)

Review 23: Subtracting by Columns (Reverse Addition)

MULTIPLICATION REVIEW

Reference: MILESTONE 4: Multiplication

Review 30: Multiplication is Repeated Addition

Review 31: Multiplication Shortcuts

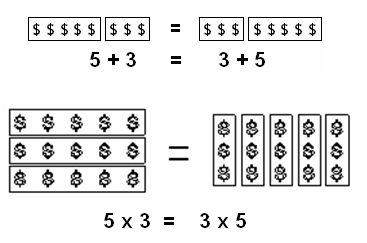
Review 32: Multiplication Properties

Review 33: Multiplying by Column

Review 34: Multiplying Large Numbers

Review 35: Math Trick Multiply Using Lines

DIVISION REVIEW

Reference: MILESTONE 5: Division

Review 40: Division is Repeated Taking Out

Review 41: Exact and Inexact Division

Review 42: Some Division Facts

Review 43: Dividing by Column

Review 44: Dividing by Large Numbers

Thinking Out of the Box