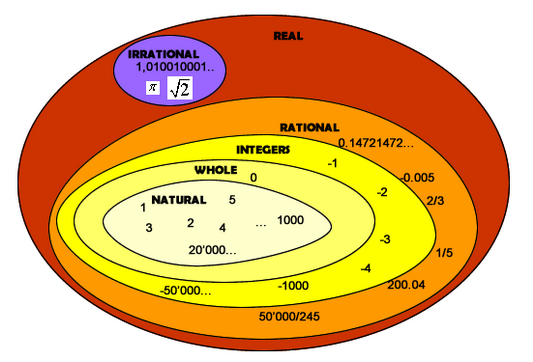
Natural numbers are counting numbers. Counting refers to things. Counting starts from 1 and goes “one more” forever.
Whole numbers include the additional idea of “nothing” as the absolute reference point. This reference point exists at the beginning of the number line as zero (0). One may then count forever starting from 0. Thus, whole numbers include natural numbers.
Whole number = 0 + natural number (in absolute sense)
Integers include the idea of a relative reference point. This reference point may exist anywhere on the number line. This reference point is also called “zero”, and one counts from this point forever in either direction. Counting to the right is positive. Counting to the left is negative. Thus, integers include whole numbers.
Positive number = 0 + natural number (in relative sense)
Negative number = 0 – natural number (in relative sense)
Rational numbers fill the gaps between integers on the number line, such as, between 0 and 1, between 1 and 2, etc. These numbers are represented as a ratio of two integers, such as, “1/2”, “2/3”, “7/4”, etc. Rational numbers include all integers. Rational numbers may be represented by decimal numbers that either are recurring or terminate.
Rational number = ratio of two integers
Irrational numbers also fill the gaps between integers, but they cannot be represented as ratio of two integers. Example of irrational number is the “circumference to diameter ratio” of a circle. This is known as “π (pi)”. Other examples are square roots of prime numbers, such as, √2, √3, etc. Irrational numbers may be approximated by decimal numbers of any length.
All the above numbers together make up the set of Real Numbers. The squares of real numbers are always positive and never negative. The square roots of negative numbers are represented by Imaginary numbers.
.

Comments
Do imaginary numbers belong on this page?
No. Imaginary numbers are not real.
But zero is unique. It is not like the counting numbers.
Zero adds an abstract aspect to the numbers.
Zero cannot be defined quantitatively.
Qualitatively, zero may be used as a reference point.
But, zero can have any number of qualities.
.
Why is 0 not placed inside the brackets of the set of whole numbers?
0 and {1, 2, 3, …} = {0, 1, 2, 3, …}
.
ah, and = plus.
The philosophy of mathematics can get a bit circular, (empty set) but the principals of arithmetic are invaluable to logical thinking.
A SET is a collection of items. When there is no item in a set then it would be an empty set.
But when a set contains 0 as a number, 0 is looked upon as an item. A set containing 0 is not an empty set.