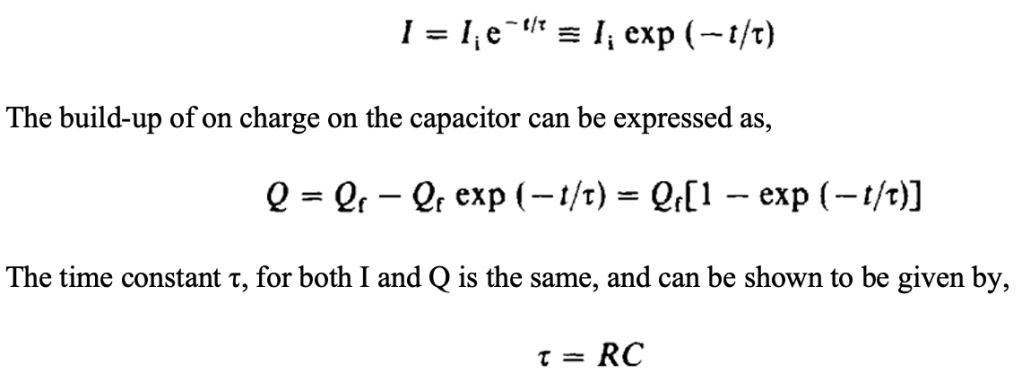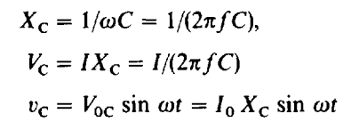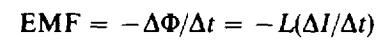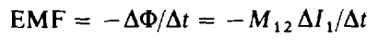Category Archives: Physics

Physics II: Chapter 11

May 20, 2023 – 6:11 AM

Reference: Beginning Physics II

Chapter 11: TIME VARYING ELECTRIC CIRCUITS

.

KEY WORD LIST

DC CIRCUIT, R-C CIRCUIT, R-L CIRCUIT, L-C CIRCUIT, AC CIRCUIT, IN PHASE, OUT OF PHASE, RMS VALUE, CAPACITIVE REACTANCE, IMPEDANCE (R-C CIRCUIT), INDUCTIVE REACTANCE, IMPEDANCE (R-L CIRCUIT), R-L-C CIRCUIT

.

GLOSSARY

For details on the following concepts, please consult Chapter 11.

DC CIRCUIT
A DC (direct current) circuit generally consists of a battery acting as the energy source, through its EMF, and causing a steady voltage to act across one or more resistors, capacitors or inductors. In the steady state, after all transient phenomena have stopped, there is no voltage across an inductor, since the current is no longer changing. There is a steady voltage across a capacitor, equal to Q/C, but there is no current flowing to or from the capacitor. The voltage across a resistor will equal V = IR.

R-C CIRCUIT
A DC circuit with a resistor R and a capacitor C shows a transient response when the switch is connected or disconnected.

At the moment the switch is closed, there is current in the circuit but no charge on the capacitor, and when the capacitor is fully charged, there is no current in the circuit. The current decays exponentially, which can be expressed as,

The situation is very similar in the case of the discharge of a capacitor.

R-L CIRCUIT
A DC circuit with a resistor R and an inductor L also shows a transient response when the switch is connected or disconnected.

In a similar manner, if current is decreasing in an L-R circuit, it will decay exponentially with a time constant L/R.

L-C CIRCUIT
In this circuit there is no dissipation of energy because there is no resistor. The capacitor stores energy in the form of separated charges or electric fields. The inductor stores energy in the form of moving charges or magnetic fields. The total energy remains in the system.

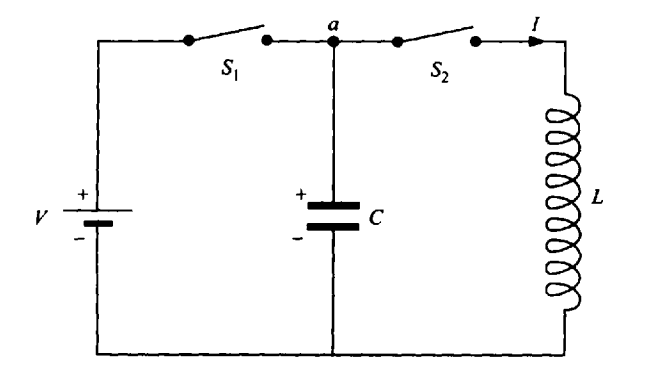
Therefore, the separated charges and the current interchange. This would be an oscillatory situation, with a repetitive interchange of energy between the capacitor and the inductor ad infinitum.

In the above circuit we first close switch S1 while S2 is open, and charge the capacitor to a voltage V, and charge Qmax. We then open S1 with the capacitor charged, and close S2 to permit the capacitor to discharge through the inductor. The capacitor discharges and then charges up again. This is similar to the case of simple harmonic motion (SHM).

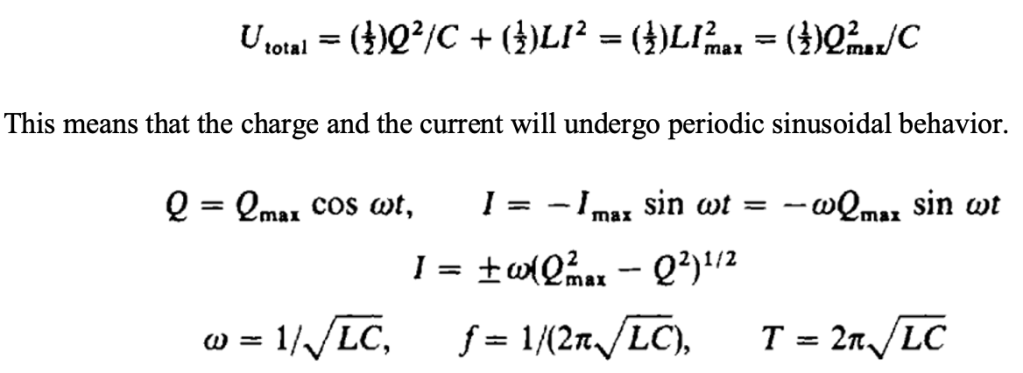
This frequency, f, is called the resonance frequency of the circuit.

AC CIRCUIT
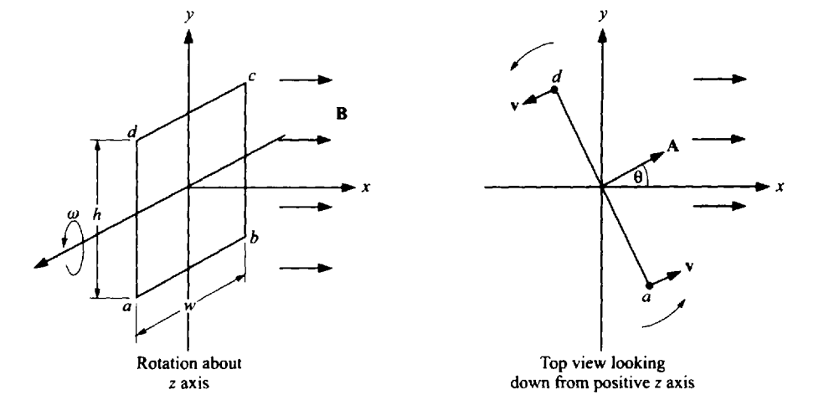
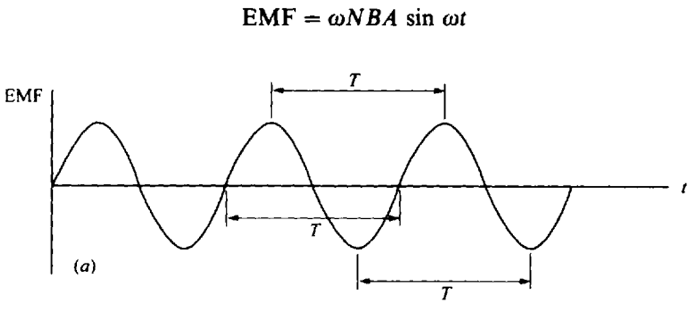
An AC (alternate current) circuit generally consists of a source of voltage that is varying sinusoidally.In that case we expect that the variables of the circuit will also vary sinusoidally, after there has been sufficient time for the circuit to reach a steady state. This time is usually short enough that the effect of the transients can be neglected.

Whenever we have sinusoidal variation, we can express the variables as sine or cosine functions of time. The frequency f of the sinusoidal variation can be expressed in terms of an angular frequency ω, which simplifies the equations. Of course, the frequency can also be related to the period, T, by the relationship f= 1/T.

IN PHASE
In AC circuit with a resistor, both current i and voltage v vary identically with time as cos ωt. We say that the two are “in phase”. This means that they both attain their maximum value at the same time, and both go through zero at the same time. We will see that this is true only for a resistor, while for capacitors and inductors, the voltage will not be in phase with the current.

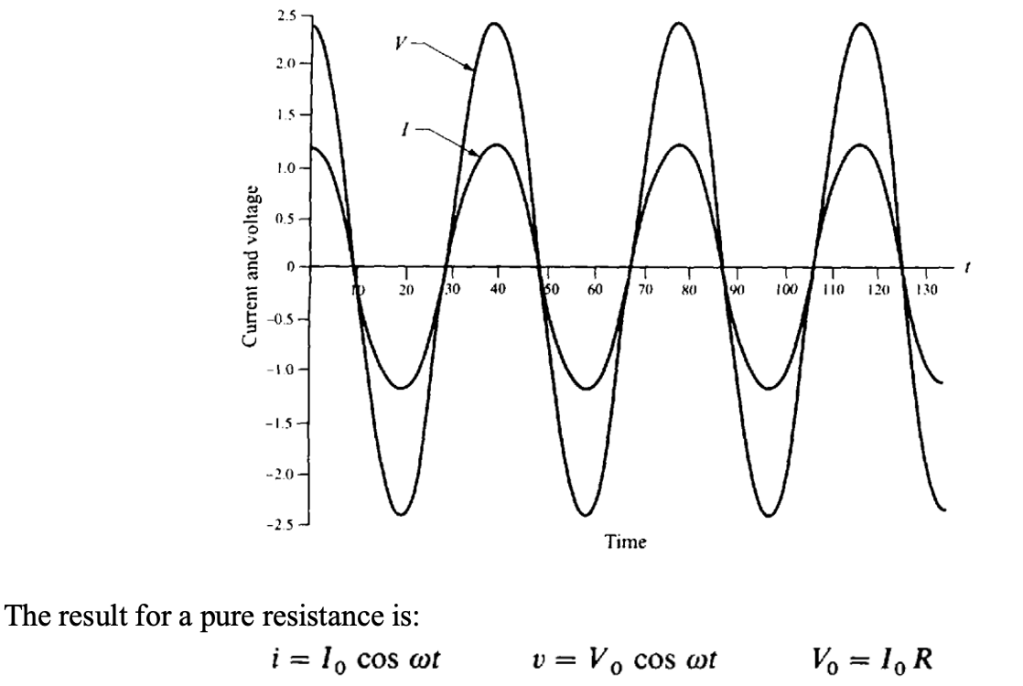
The voltage at any time is just a fixed multiple of the current.

OUT OF PHASE
When a generator causes a sinusoidal current to flow through the capacitor given by i = I0 cos ωt the capacitor is alternately charging each plate positively and negatively at a frequency: f = ω/2π. The voltage across the capacitor is defined to be from positive to negative plate and is always given as v = q/C. Both v and q will vary sinusoidally at the same frequency as the current. When the voltage reaches its peak, the current is zero. The current and voltage are said to be 90° or π/2 out of phase, and the current “leads” the voltage. We thus know that, for a capacitor, we can represent the voltage by v = VI0 sin ωt if the current is given by i = I0 cos ωt.

RMS VALUE
In most formulas used in AC circuits, the quantity we use for the “magnitude” of currents and voltages will be the RMS value, and therefore when we write just I or V we will refer to the RMS values. The term RMS actually stands for “root-mean-square”, which refers to the method used to determine its value. To get the RMS value of a variable, we have to take the square root of the average (mean) of the square of the quantity.  The current will vary as i = I0 cos ωt. I0 is the amplitude of the variation, and it represents the maximum value the current can have. We have the “RMS” value: IRMS = I0 √2.

CAPACITIVE REACTANCE
We expect that if the maximum current is increased then the maximum charge on the capacitor will increase proportionally, and therefore also the maximum voltage. Consequently, we can write that V0 = χcI0, where the constant of proportionality χc is called the capacitive reactance of the capacitor. Similarly, VRMS = χcIRMS, or V = χcI. This capacitive reactance depends on the capacitance and on the frequency. Therefore, we have,

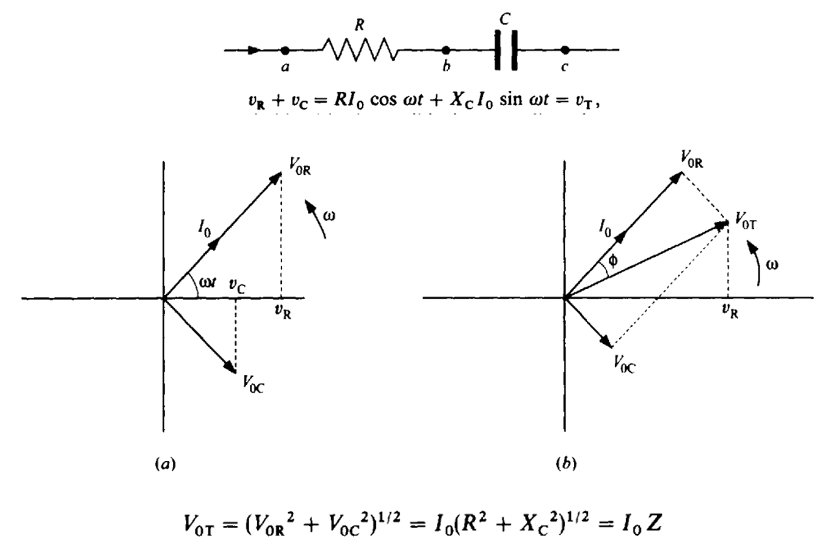
IMPEDANCE (R-C CIRCUIT)
When the Resistor and Capacitor are in Series, with the current given by as i = I0 cos ωt, the voltage across the entire circuit is

INDUCTIVE REACTANCE
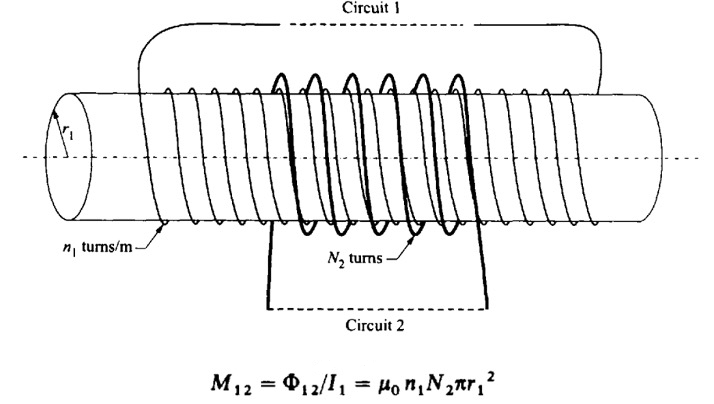
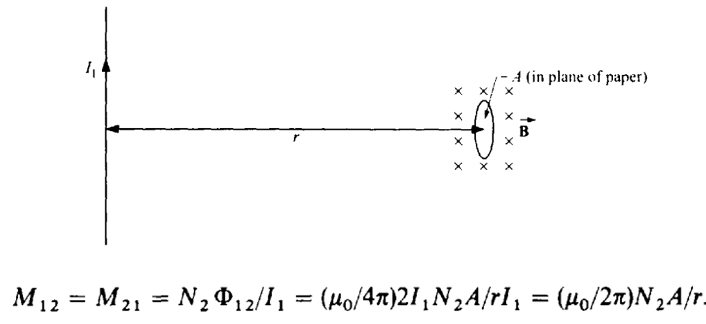
An AC generator produces a current I = I0 cos ωt in the inductor. The inductor produces a back EMF equal to (- L ∆I/∆t). This back EMF is balanced by the electrostatic voltage across the inductor, vL, as shown in the figure.

The voltage across the inductor is 90° out of phase with the current. The voltage leads the current,

IMPEDANCE (R-L CIRCUIT)
When the Resistor and are in Series, with the current given by as i = I0 cos ωt, the voltage across the entire circuit and impedance is given by

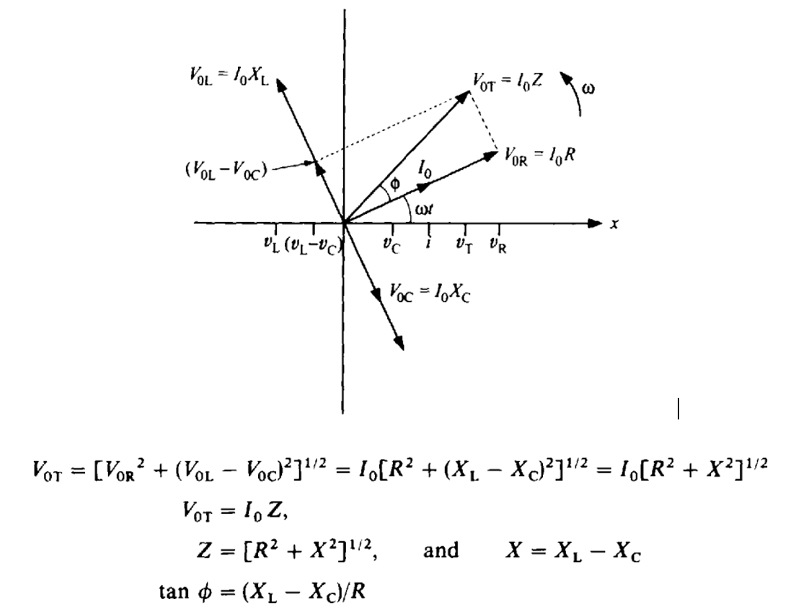
We see that cos φ is again the power factor for an R-L circuit as it was for an R-C circuit. We can generally write that cos φ = X/R, where X is the reactance of the circuit, and equals XL for a circuit with inductance and -XC for a circuit with capacitance. Similarly, the impedance can then be written as Z = (R2 + X2)1/2, which will be valid for both R-C and R-L circuits. Additionally, we can write that the total voltage will vary with time as vT = V0T cos (ω t + φ), both for the case of the R-C and the R-L circuits, For the R-C circuit, φ is negative, and in the R-L circuit, φ is positive. We will find that we can extend these ideas to the last case, the R-L-C circuit also.

R-L-C CIRCUIT
Here we have Resistor, Inductor and Capacitor in Series. We can write the equations giving these respective voltages as functions of time as:

From the phasor diagram we can deduce other relationships:

.

By vinaire | Comments (0)

Physics II: Chapter 10

May 16, 2023 – 9:11 AM

Reference: Beginning Physics II

Chapter 10: INDUCTANCE

.

KEY WORD LIST

Self-Inductance, Mutual Inductance, Inductor, Energy in an Inductor, Energy Density in Space, Transformers

.

GLOSSARY

For details on the following concepts, please consult Chapter 10.

SELF-INDUCTANCE
Self-inductance arises from the flux that a current circuit produces within its own area. It is distinguished from mutual inductance. Self-inductance depends only on the geometry of the circuit. It connects the flux with the current as follows,

The unit for inductance is Wb/A, which is given the name henry. Practical circuits have inductance much smaller than one henry, more in the range of millihenries. The main use of the concept of inductance will be in circuits where the current changes, thus causing a proportional change in flux. This changing flux induces an EMF:

Solenoid
The self-inductance, L, of the solenoid is: L = μ0 n2Ad; and the inductance per unit length is:
L/d = μ0 n2A.

Toroid
The self-inductance, L, of the solenoid is: L = μ0 N2A/2πr. If the toroid is filled with material of permeability μ, then: L = μ N2A/2πr.

MUTUAL INDUCTANCE
Whenever one has two circuits near each other, it will be possible for a current which exists in one circuit to produce flux through the second circuit. If φ12 is the flux in circuit 2 caused by a current I1, in circuit 1, Then, the mutual inductance, M12, connects these two quantities, as follows,

The exact value of M12 is determined by the geometrical relationship between the two circuits. The change in current in circuit 1 changes the flux in circuit 2 proportionally, which produces an EMF in circuit 2, given by

There is only one mutual inductance for the two circuits meaning M12 = M21. We can measure the mutual inductance by measuring the induced EMF produced in one circuit by a known rate of change in current in the other circuit.

Coil on Solenoid

Coil on Toroid

Coil Near Long Wire

Coil at Center of Loop

INDUCTOR
Any circuit element that generates an inductance when current flows through it (e.g. a coil, a solenoid, a toroid) is called an inductor. An inductor has the property that it produces a back EMF if the current is changing, but does nothing if the current is steady. While an inductor will not affect a DC circuit once a current has been established it will be of great importance during the time that the current is being turned on or off.

ENERGY IN AN INDUCTOR
In order to increase the current in the inductor, an external driving voltage must be imposed on the circuit to overcome the back EMF, and this voltage will do work against the resisting EMF. The voltage will continue to do work until the current reaches its final value, at which time the current is no longer changing and no back EMF is being produced. During the time that the current is building up from zero to its final value, however, work must be done on the inductor. The work, or energy stored in the inductor is,

This result is similar to the case of storing energy in a capacitor by virtue of the charge that we have placed on the plates of the capacitor. There the energy stored = (1/2)Q2/C.

In terms of the magnetic field that have been set up in space, we have,

At any point in space, where there is a magnetic field, a certain amount of energy is stored. This energy equals the energy density times the volume of space being considered. The same general consideration holds for electric fields as well and indeed the electric field energy density is given by (1/2) ε0E2. In other words, wherever electric or magnetic fields exist in space, energy is being stored in the form of these fields

ENERGY DENSITY IN SPACE
The total energy density at any point in space is the sum of the electric and the magnetic field energy densities. Since the units for energy density are the same irrespective of their source, this offers a means of comparing the relative magnitudes of electric and magnetic fields. Electric and magnetic fields with the same energy density can be considered to be comparable to each other. The electric and the magnetic fields associated with electromagnetic waves have equal energy densities. These considerations lend credence to the idea that these fields are real physical quantities that actually exist in space and are not merely mathematical contrivances that make it easier to calculate the forces exerted by the electric and magnetic interactions.

TRANSFORMERS
We can induce EMFs in one circuit by changing the current in another circuit. This forms the basis of the transformer, which is used to transform voltage in one circuit into a different voltage in a second circuit. All the magnetic flux established by the first winding, called the primary coil, passes through the turns of the other winding, called the secondary coil. In order to get large fluxes, it is useful to place ferromagnetic material within the solenoid that has a large permeability, such as iron. The figure below shows a typical transformer:

Here, the primary winding, with N1 turns, is wound on one side of the rectangular ring, and the secondary winding, with N2 turns, is wound on the other side of the ring. This is a typical transformer. If one changes the voltage in the primary circuit, the current in the primary circuit will change, and therefore the flux. For a perfect transformer, the flux through one turn of the secondary is the same as the flux through one turn of the primary. Therefore, the total EMF developed in each winding will depend on the number of turns in that circuit.

A transformer is useful only with currents that are changing, as with AC. In that case, it is possible to use a transformer to convert a voltage applied to the primary circuit into a larger or smaller voltage in the secondary circuit. This ability to easily convert (transform) voltages in AC, which is much more difficult for DC, is the main reason why AC is the primary source of power throughout the world.

.

By vinaire | Comments (0)

Physics II: Chapter 9

May 12, 2023 – 11:56 AM

Reference: Beginning Physics II

Chapter 9: INDUCED EMF

.

KEY WORD LIST

Generator, Motional EMF, Induced EMF, Magnetic Flux, Faraday’s Law, Lenz’s Law, Alternating Current, Direct Current, Induced Electric Fields

.

GLOSSARY

For details on the following concepts, please consult Chapter 9.

GENERATOR
When a wire moves through a magnetic field an EMF is generated in the wire, which has the ability to move charges through the wire. This means that it is possible to build an apparatus that makes use of magnetic effects to produce EMFs that drive electrical circuits connected to the apparatus. The apparatus is called a generator, and, like a battery, it pumps positive charges within the apparatus toward the high-potential end of the apparatus, so that, in an external circuit, the charges produce a current flowing from the high- to the low-voltage terminals. As in a battery, the voltage produced by the generator on open circuit is its EMF.

MOTIONAL EMF
An EMF produced in wires moving through a magnetic field is called motional EMF. For a wire of length L, with uniform electric field E, the potential difference is Vba = EL, and using the relation result E = vB, we have for our moving wire:

INDUCED EMF
An EMF produced in stationary wires that are situated in a changing magnetic field is called induced EMF. Its characteristics are given by Faraday’s law.

MAGNETIC FLUX
It is a concept similar to electric flux. As in the case of electric flux one can visualize the magnetic flux by drawing magnetic field lines, with the number of field lines passing through a unit area perpendicular to the lines proportional to B at that location.

In the following diagram there is a small planar area A represented by a vector A that has a magnitude equal to the area, and a direction perpendicular to the plane of the area. We use the notion of circulating current and the right and rule to determine the positive direction of A. For a magnetic field B that passes through the area in the positive direction at an angle θ to A, we define the magnetic flux as

The total magnetic flux through any area is just proportional to the total number of field lines through that area. The unit for magnetic flux is T – m2, which is given the name Weber (Wb).

FARADAY’S LAW
This law says that whenever there is a change in flux within a circuit there will be an EMF induced in the circuit. This EMF depends on the time rate of change of the flux through the circuit,

where ∆φ is the change in magnetic flux through the circuit in a short time interval, ∆t. The minus sign is necessary to assure that the correct direction is given for the EMF. The requirement of the minus sign is called Lenz’s law.

LENZ’S LAW
This law states that the EMF produced by a changing flux is always in a direction to produce a current whose own flux is in the opposite direction to the initial change in flux.

ALTERNATING CURRENT
One can generate an EMF by rotating a coil with an angular velocity ω in a magnetic field B. Then the angle θ = ωt. The flux (φ) through a single turn of the coil is given by BAcos θ, or BAcos ωt.

By differentiating, we get the EMF to be,

The EMF varies as sin ωt. The EMF produced in this manner will change its direction and then change back again at an angular frequency ω, or at a frequency f = ω/2π and period T = 2π/ω. This is what we call an alternating voltage which produces an alternating current (AC). Thus, by rotating a coil in a magnetic field, we can easily generate an AC voltage. The magnitude of the voltage can be increased by constructing the coil out of many turns, N, of wire, in which case the voltage becomes,

DIRECT CURRENT
It is also possible to construct generators to produce DC (direct current) voltage. To accomplish this, we reverse the connection to the outside wires every time the direction of the EMF in the coil reverses direction. The resultant EMF in the outside circuit will then take the form shown below.

Secondly, we use several coils (armature), in which each coil will produce a voltage which reaches its maximum at a different time, and the total voltage will vary very little with time.

INDUCED ELECTRIC FIELDS
Any changing magnetic field actually produces a new type of electric field in the vicinity of the circuit that pushes the charges and creates the EMF in the stationary circuit. This new electric field is fundamentally different from the “electrostatic” field produced by point charges. . Thus, Faraday’s law has profound implications for our concept of the electric field.

.

By vinaire | Comments (0)

Physics II: Chapter 8

May 8, 2023 – 5:58 PM

Reference: Beginning Physics II

Chapter 8: MAGNETIC PROPERTIES OF MATTER

.

KEY WORD LIST

Magnetization, Orbital Motion, Spin, Diamagnetic Material, Paramagnetic Material, Ferromagnetism, Magnetic Poles, Magnetization Vector, Magnetic Intensity Vector, Magnetic Susceptibility, Superconductor

.

GLOSSARY

For details on the following concepts, please consult Chapter 8.

MAGNETIZATION
A magnetic field can change the properties of the material in which it is created, and result in having the material produce its own field, which has to be added to the original field. This modification of the properties of a material is called “magnetization” of the material.

ORBITAL MOTION
In order for a magnetic field to have any effect, a material must consist of moving charged particles. All materials consist of a collection of atoms and molecules. The orbital motion may be thought of as electrons circulating about a nucleus within an atom.

SPIN
In addition to orbiting the nucleus, the electrons spin on their axes and, as a consequence, have an additional “spin” angular momentum and “spin” electric current loops. In either case, orbital or spin, magnetic fields can be set up by the atomic current loops, and an external magnetic field can exert forces on the electrons, and thereby modify their motion.

DIAMAGNETIC MATERIAL
An external magnetic field generally induces      currents and associated magnetic moments in the atoms of a material. These magnetic moments, in turn, produce their own magnetic fields, which, by Lenz’s law, are in a direction opposite to the original field. The materials in which this is the dominant effect are called diamagnetic materials, in the same manner as materials that produce electric fields opposed to the original electric field are dielectric materials. In general, such induced magnetic fields in an atom are very small and the external field is reduced by a tiny amount as a consequence of diamagnetism. While diamagnetism is present in all atoms, it dominates only in those atoms in which the orbital and spin angular moments average out to zero.

PARAMAGNETIC MATERIAL
In paramagnetic materials there is a net orbital and/or spin angular momentum and a net effective current loop for the atom. Such an “effective” current loop gives the atom a definite overall magnetic dipole moment. An external magnetic field exerts a torque on such a magnetic moment and the torque tries to line up the moment parallel to the magnetic field. The lined-up moments will then produce their own magnetic field in the same direction as the original field, thus increasing the magnetic field. Paramagnetic materials are more common than diamagnetic materials, especially since they dominate in materials where both effects are present.

FERROMAGNETISM
Certain materials, notably iron, nickel and cobalt, exhibit ferromagnetism at room temperature. This means that the magnetic interactions between the magnetic moments of neighboring atoms is strong enough, even at room temperature, to align the moments in the same direction. If an external field is applied to the ferromagnetic material it has the effect of causing the domains of aligned moments to rotate and point in the same direction, the direction of the magnetic field. Once they have been aligned, they tend to remain aligned even if the external field that originally caused them to align is removed. The material has now become a permanent magnet.

MAGNETIC POLES
The field produced by a solenoid is nearly the same in shape as the electric field produced by oppositely charged particles located at the ends of the bar. We therefore often talk of the bar as being composed of two opposite magnetic poles (the substitute for electric charges), one called a north pole and the other called a south pole.

The north pole is the apparent source of magnetic field lines (as is a positive charge for electric field lines), and the south pole is a sink for the lines. In actuality the lines do not terminate at the poles, but continue in straight lines within the material, forming closed loops. The designation of north or south pole arises from the fact that the bar tends to line up in the magnetic field of the earth with the north pole facing in the northerly direction. As in the case of electric charges, opposite poles attract, and similar poles repel each other.

MAGNETIZATION VECTOR
The magnetization vector, M, is the total magnetic moment per unit volume. Thus, a material in a magnetic field can become magnetized, with a magnetization M = ΣM/V). The magnetic field, BM produced by the magnetic dipoles in the material is related to the magnetization as follows.

MAGNETIC INTENSITY VECTOR (H)
It is the part of the magnetic field in a material that arises from an external current and is not intrinsic to the material itself. The definition of H is:

H = B/μ0 − M

where B is the actual magnetic field within a material considered as a concentration of magnetic field lines per unit cross-sectional area; μ0 is the magnetic permeability; and M is the magnetization vector. The magnetic field H might be thought of as the magnetic field produced by the flow of current in wires and the magnetic field B as the total magnetic field including also the contribution M made by the magnetic properties of the materials in the field. When a current flows in a wire wrapped on a soft-iron cylinder, the magnetizing field H is quite weak, but the actual average magnetic field (B) within the iron may be thousands of times stronger because B is greatly enhanced by the alignment of the iron’s myriad tiny natural atomic magnets in the direction of the field.

MAGNETIC SUSCEPTIBILITY
In general, except for material that becomes a permanent magnet, the magnetization is proportional to the magnetic field, and therefore to the magnetic intensity as well. We can therefore write that,

Where χ is called the magnetic susceptibility of the material. Then

where μ is the permeability of the material, κm, is the relative permeability of the material, and μ = μ0κm, with κm = 1 + χ. This means that for these materials, we can calculate B if we know H, merely by multiplying H by μ.

SUPERCONDUCTOR
Some materials, at sufficiently low temperatures lose all their resistivity. These materials are called superconductors. They also set up surface currents in a magnetic field, which themselves produce an exactly opposite field, and thereby cancel any field which tries to be established in its interior. Thus, a superconductor can be considered to be a perfect diamagnet.

.

By vinaire | Comments (0)

Physics II: Chapter 7

May 5, 2023 – 5:02 PM

Reference: Beginning Physics II

Chapter 7: MAGNETISM-SOURCE OF THE FIELD

.

KEY WORD LIST

Magnetic Field (Source), Field Produced By Currents, Solenoid, Magnetic Field Lines, Composite Fields, Ampere’s Law, Coaxial Cable

.

GLOSSARY

For details on the following concepts, please consult Chapter 7.

MAGNETIC FIELD (SOURCE)
One basic origin of a magnetic field is a moving charge or an equivalent current in a wire. It exerts a force on another moving charge. Another basic source for a magnetic field is an electric field that varies with time.

The following is the formula for the magnitude of the field produced by a moving charge q, moving with velocity v, at a point located at a displacement r from the charge.

This is known as the Law of Biot and Savart. The field is zero if φ is zero. The largest magnetic field is produced when φ is 90°. The magnitude of B decreases as 1/r2 with the distance from point a. The field increases with both q and v.

The direction of the field is perpendicular to the plane containing both v and r, and according to the right-hand rule.

If one traces the magnetic field lines, they form concentric circles around the direction of v.

Two charges of the same sign moving parallel to each other in the same direction shall experience magnetic attraction.

FIELD PRODUCED BY CURRENTS
Current flowing in a wire is equivalent to moving charge: qv = I∆L. The magnitude of the magnetic field produced by a current I flowing in a wire of length ∆L at a point located at a distance r from the element is,

Field at the Center of a Current Carrying Ring

A current I, flowing in the clockwise direction. Then the field at the center of the ring, with direction into the paper is,

For N turns of the coil the field is multiplied by N.

Field Along the Axis of a Ring

The field at the center of the ring, with direction at P to the right is,

Field of a Long Straight Wire

I is the current in the wire and R is the perpendicular distance of the point P from the wire. The direction of the field is into the paper at P.

SOLENOID
A solenoid is a wire is continuously wound around a long pipe with adjacent windings close to each other. The field within a long solenoid is the same at any point within the solenoid and is zero (or very small) outside the solenoid.

where n is the number of turns per meter. The direction of the field is parallel to the axis with the direction given by the same right-hand rule used for the ring. The result is the reason that solenoids are so very useful for producing magnetic fields. The field produced is uniform, with the same magnitude and direction everywhere within the solenoid. Furthermore, this uniform field does not depend on the radius of the solenoid, only on the number of windings per unit length. One can, for instance, wind several layers of turns, one on top of the other, to increase n, and each layer will contribute the same field, independent of the radius (as long as the solenoid is truly long).

If the solenoid is not infinitely long, but the length is much greater than the radius, then the above result is still nearly true as long as one is not too near to the end of the windings. The field lines inside the solenoid are straight lines, parallel to the axis, until one approaches the ends. Outside the solenoid, the field is no longer zero, and the field lines are as shown above. This happens to be the same field line configuration as for a permanent bar magnet.

MAGNETIC FIELD LINES
The magnetic field lines form closed loops, unlike electric field lines that begin or end at a point charge. The fact that magnetic field lines don’t converge to or diverge from a point is a fundamental property of the magnetic field and can be stated as a general law: “Magnetic field lines never converge to a point or diverge from a point”.

COMPOSITE FIELDS
If several wires each produce magnetic fields, then the actual magnetic field at any point is the vector sum of the fields produced by each wire.

AMPERE’S LAW
There is a powerful general law relating the magnetic field and the current, which often gives insight into the behavior of the magnetic field, and, in certain circumstances, allows for the compete determination of the field without lengthy calculation. This relationship is given by Ampere’s law.

The line integral of B cos θ ∆L around a closed path equals the total current flowing through the area enclosed by that path. This very important result is Ampere’s law.

COAXIAL CABLE
A coaxial cable consists of an inner solid conductor of radius R1, carrying current I out of the paper, and an outer, concentric hollow cylinder, of radius R2, carrying the same current I into the paper, the current being distributed uniformly around the cylinder.

Since the two currents are equal and flow in opposite directions, the field outside the cable is zero.

.

By vinaire | Comments (0)