Vinaire's Blog

Reference: The Book of Mathematics

Introduction

This video explains counting and the Rule of Abacus.

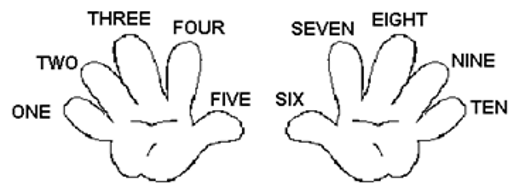
Mathematics starts with Arithmetic, and Arithmetic starts with counting. We learn to count on our fingers as follows.

We have two hands with a total of ten fingers. We can count with these fingers to find out how many things there are.

But to count beyond ten, it requires many hands. Alternatively, we can use an Abacus.

.

The Abacus

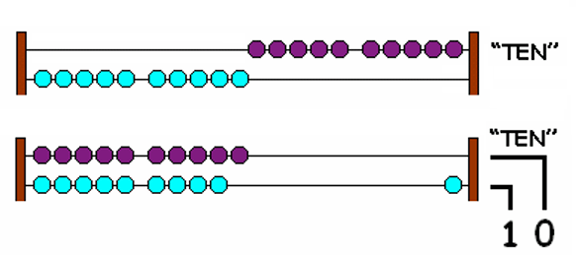
An abacus is a counting board on which one can count to very large numbers. It has many wires. On each wire there are ten beads.

The count appears on the abacus when beads are moved to the right. The count on a wire is the number of beads on the right.

.

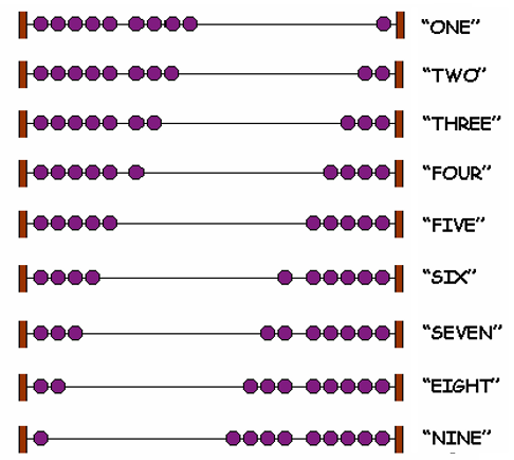
The Rule of Abacus

“When all beads are counted to the right on a wire, they are replaced by counting one bead to the right on the next wire.”

Obviously, when there is no bead on the right, the count is zero.

.

Counting beyond Ten

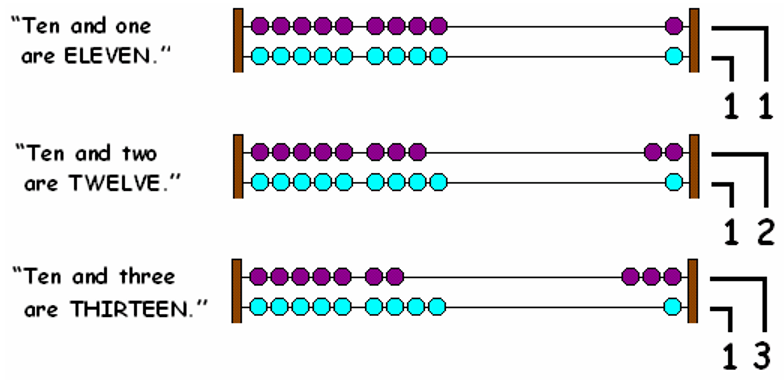
We count beyond 10 by moving beads on the first wire again.

Today, we may not use the abacus, but we still use the Rule of Abacus in our numbering system.

After 19, the next number is 20.
After 29, the next number is 30.

…

After 89, the next number is 90.
After 99, the next number is 100.

.

Computers and Binary Numbers

In our computers we use the numbers made up of 0’s and 1’s. These binary numbers may be created on an abacus that has only 2 beads on each wire. The Rule of Abacus applies to this “binary abacus” also.

The number of beads on a wire represent the “base” of the numbering system.

If you imagine an abacus with two beads on each wire, it will use the digits 0 and 1 only, because when two is counted the rule of abacus will apply and the number “two” will appear as “10”. The number “three” will appear as “11”.  At “four” the rule of abacus will be applied twice. The number “four” will appear as “100”. You may construct all binary numbers this way.

.

Check your Understanding

1. What is Counting?

The traditional way of counting consists of calling the first item as ONE, the next item as TWO, and so on. Counting can go on forever.

.

2. What is the Rule of Abacus?

The RULE OF ABACUS is, “When all beads are counted to the right on a wire, they are replaced by counting one bead to the right on the next wire.”

.

3. How is the Rule of Abacus helpful?

You need only as many digits to write the numbers as there are beads on a wire of abacus. One of those digits is always 0 (Zero). This is very useful when there are only two polarities to represent numbers as in the case of electronic computers.

.

Final Thoughts

The very fact of counting makes mathematics fundamentally discrete. It cannot duplicate continuous reality, such as, the reality of PI (𝜋).

Reference: The Book of Mathematics

Introduction

In this video we are going to look at what mathematics is. Let’s start with a quiz.

We all have studied mathematics. Do you know what the word MATHEMATICS means?

The word MATHEMATICS comes from a Greek word, máthēma, which has the concept of “learning” or “knowing”. “Knowing” is very different from memorizing. You get the sense of “knowing” when you learn to ride a bike.

.

We all had to study mathematics in school. What is the real reason for studying mathematics?

You study mathematics to develop the ability to think systematically. It is much more than learning to avoid being shortchanged.

.

How does one learn to think systematically with mathematics?

The basic concepts of mathematics like numbers and counting make you think systematically when solving problems. Solving math puzzles is a great way to practice math creatively.

.

Examples

Here is an example of thinking creatively with numbers.

A man gave his son the following riddle. “Take a 5-gallon and a 3-gallon bucket down to the lake and bring back exactly 4 gallons of water.” How will you solve this riddle?

SOLUTION:

1. Fill the 3-gallon bucket and empty it in the 5-gallon bucket.
2. Fill the 3-gallon bucket again and pour it till the 5-gallon bucket is full. You will have 1 gallon of water left in the 3-gallon bucket.
3. Empty the 5-gallon bucket back into the lake and pour 1 gallon of water into it from the 3-gallon bucket.
4. Fill the 3-gallon bucket and empty it in the 5-gallon bucket.
5. You now have 4 gallons of water in the 5-gallon bucket.

3 + 3 – 5 + 3    =      4 gallons  (Answer)

.

Math teaches you to visualize the problem when solving it. Here is an example.

A waterlily doubles itself in size each day. From the time its first leaf appeared to the time when the surface of the pond was completely covered took forty days. How long did it take for the pond to be half covered?

SOLUTION:

• During the last and fortieth day the pond which was half covered becomes completely covered – just doubled in one day.
• Therefore, the pond was half covered the previous day – the 39th day.

So, it took 39 days for the pond to be half covered.                 Answer

.

Math teaches you not to assume anything about the problem when solving it. Here is an example.

There are three books, each one inch thick. They stand side by side in order – Volumes I, II, and III. A bookworm starts outside the front cover of Volume I and eats its way through to the outside of the back cover of Volume III. If the worm travels in a straight line, how far does it travel?

SOLUTION:

• Check out 3 books on a bookshelf. The outside of the front cover of Volume I is actually in contact with Volume II, and so is the outside of the back cover of Volume III.
• So, the worm travels only through the thickness of Volume II.

The worm travels one inch.                                      Answer

.

Check your Understanding

Why should you study mathematics?

You study mathematics to improve your ability to think systematically.

.

See if you can solve the following puzzle:

If it takes 6 minutes to saw a log into three pieces, how long will it take to saw that log into four pieces?

It takes 2 cuts for 3 pieces; therefore, each cut takes 3 minutes. It takes 3 cuts for 4 pieces. 3 cuts will take 9 minutes. The answer is 9 minutes.

.

Final Thought

Hope you now have a better understanding of what mathematics is.

The key take away is that mathematics has to do with KNOWING and not memorizing. It helps you develop the ability to think systematically.

.

The above is a very instructive problem and solution.