Reference: Einstein’s 1920 Book
Appendix I
Simple Derivation of the Lorentz Transformation
Please see Appendix 1 at the link above. This appendix is supplementary to Section XI.
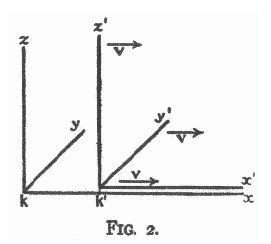
The Fig. 2 above provides the relative orientation of the co-ordinate systems K and K’. K is relatively at “rest” while K’ is moving at a velocity v.
The coordinates of K and K’ are different for the same event, but they are related by the fact that the velocity of light c is the same in both coordinate systems.
The coordinates for an event in K shall be related by constants to the corresponding coordinates in K’ because v is constant. This is true for motion in reverse direction for straight line motion.
We can relate the uniform velocity v to the constants involved in the correspondence of the coordinates of K and K’.
According to the principle of relativity the unit of lengths at rest in K or K’ will appear to be the same when viewed from the other system (K’ or K). From this we can determine the value of the constants involved in terms of v and c.
This gives us the following relationships between the coordinates of K and K’.
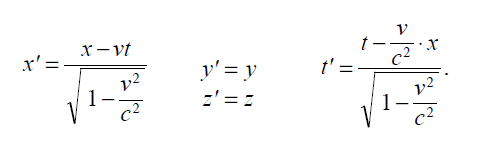
In this way we satisfy the postulate of the constancy of the velocity of light in vacuo for rays of light of arbitrary direction, both for the system K and for the system K’. We have thus derived the Lorentz transformation.
.
