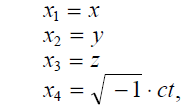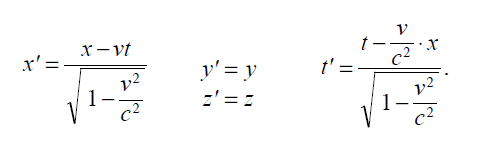Category Archives: Einstein

Space, Mathematics and Einstein

November 4, 2025 – 5:23 AM

Einstein, in his general relativity, gives pure space a structure. This structure is influenced by the presence of physical mass. Where does this structure of space come from?

Space can curve. If this is an analogy, then the only description of space curving is through mathematics. Mathematics is based on postulates that are in coherence with each other. These postulates, axioms, or rules are all pure thought

So, a structure for pure space is being postulated in GR. Light is shown to follow this structure. Gravity of planets is also explained when planets are seen to follow this structure of pure space.

Basically, GR is postulating a coherence between physical structure of matter and radiation on one hand and the structure of pure space on the other. Matter, radiation and “space” are shown to be in some kind of coherence, or equilibrium, with each other.

We can sense the physical structures of matter and radiation through our physical senses. But we can sense the structure of pure space only through the thought put in mathematics. We can sense thought through our mental sense. And this makes thought a substance on its own right.

This is because SUBSTANCE can be defined as “anything substantial enough to be sensed.” We sense thought differently from radiation and matter; but thought, radiation and matter can all be sensed.

We may, therefore, say that pure space is made of thought.

.

By vinaire | Comments (4)

Introduction (Relativity)

July 17, 2024 – 6:35 AM

Reference: Einstein 1920: Relativity

Einstein starts with considering the coordinates of space and time that have so far been considered in an abstract mathematical sense, and applies to them the principles of palpability of physics. Matter, in spite of being very rigid, expands and contracts when heated and cooled. Can the rigid coordinates of space also expand and contract under the influence of time? So started the thought that went into building a fantastic theory of relativity.

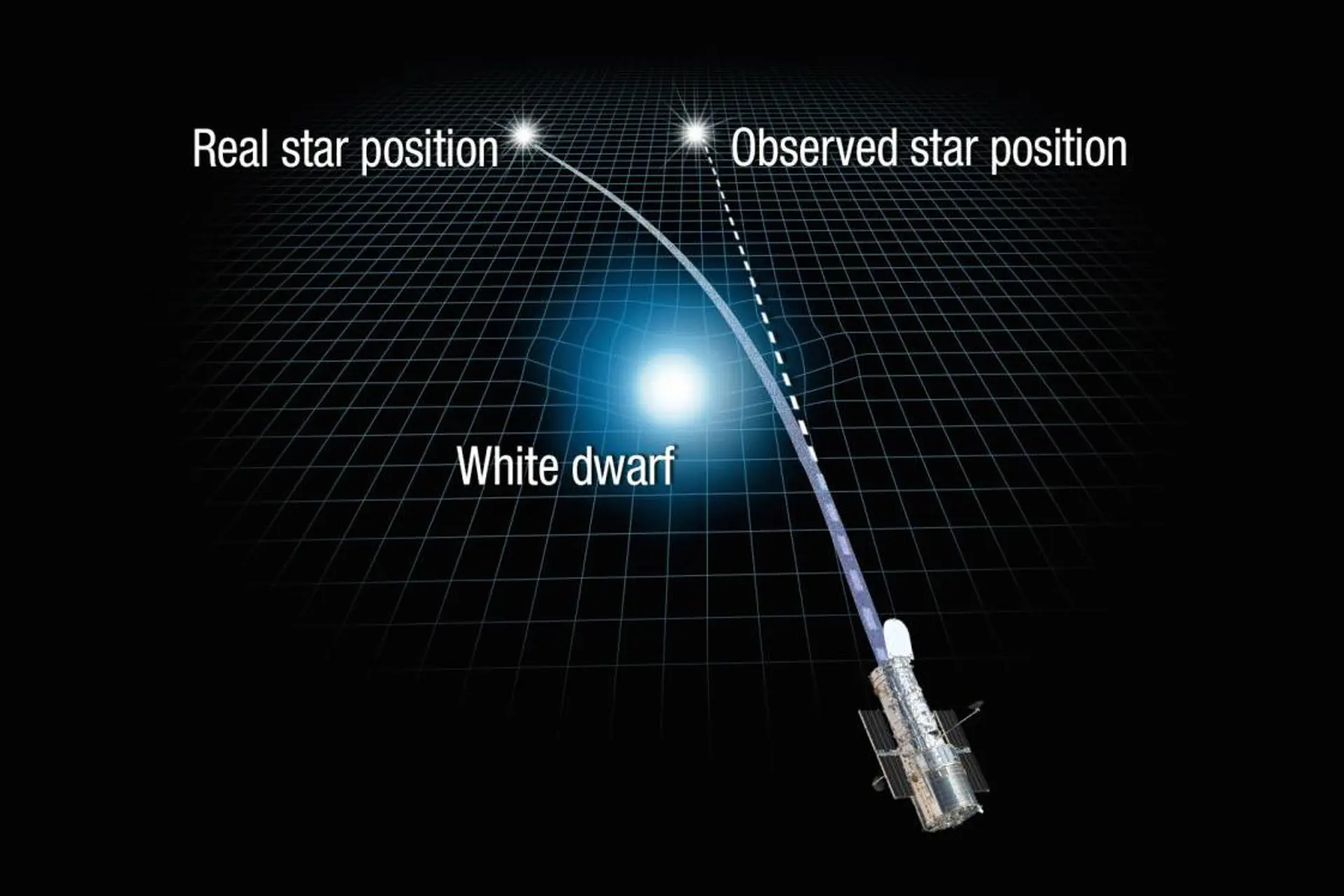
The theory of relativity presents a fascinating view of the physical universe. It presents the covariance of space, time and substantiality in the form of a four-dimensional world. Under the influence of time, space seems to acquire the palpability of substance. The concept of substance includes both the rigidity of matter and the fluidity of energy. For example, Matter becomes concentrated energy, and energy becomes diluted matter. The concept of inertia that applied to matter in classical mechanics, now gets generalized into the consistency of space. The variability of this consistency makes space appear as energy and matter in a gravitational field.

The comments at the end of this book present the following model of the universe based on Einstein’s theory of relativity:

The space has substantiality, which gives it a measure of consistency. When the consistency is extremely small, the space appears as fluid energy that has a very high velocity. When the consistency is extremely large, the space appears as rigid matter that has a very low velocity. In between, the space appears as the gravitational field of variable consistency and velocity. The velocity has an inverse relationship with consistency. It is the balance of inherent motion of matter floating in a sea of energy that is perceived as the phenomenon of Gravity.

The spectrum of energy/matter based on the property of consistency suggests a vortex type pattern, which is seen repeated in nature at all scales. For example, the atoms display this pattern where the electrons form a vortex, at the center of which there is an extremely dense and small spinning nucleus. The “gravitational field” at this level appears as charge.

At the level of the solar system, planets revolve, as if they are caught up in a vortex of gravity, at the center which is a massive and spinning sun. In their turn, the spinning planets form the center of smaller vortices of gravity in which their moons are caught up.

On a much larger cosmic scale, we have solar or star systems that are caught up in a vortex of gravity which appears as a galaxy. At the center of the galaxy is an extremely dense and small spinning black hole.

All these vortices at different scales seem to be overlapping and producing a very complex pattern in which the inherent motions of the heavenly bodies balance each other in a cosmic dance. We may thus visualize the universe having a “solid” spinning center made up uncountable number of galaxies with a great periphery of curving light far away of unimaginable proportions.

This “vortex universe” is devoid of solid masses in about 99% of its volume; but that volume is filled with palpable energy. The universe may be considered to be finite yet unbounded because it seems to curve upon itself.

.

By vinaire | Comments (0)

Preface (Relativity)

July 16, 2024 – 8:07 PM

Reference: Einstein’s 1920 Book

This Book summarizes Albert Einstein’s RELATIVITY: THE SPECIAL AND GENERAL THEORY, originally published by Henry Holt and Company, New York (1920).

Einstein’s Special Theory of Relativity addresses the effect of the finiteness of the velocity of light on the space coordinates. A much more comprehensive General Theory of Relativity then explains gravity by postulating a four-dimensional continuum that has acquired the properties of extension and durability.

This book summarizes the original presentation above one section at a time. The summary contains Einstein’s ideas in their purity.

The summary is accompanied by comments, also one section at a time, that provide a new interpretation of Einstein’s ideas. This interpretation gradually builds up a model of the universe that makes Einstein’s theory of relativity easier to understand.

It is my hope that more people will get the pleasure of really understanding this brilliant theory of relativity that was completed by Einstein in 1915.

.

By vinaire | Comments (0)

Einstein 1920 (App II) Minkowski’s Four-Dimensional “World”

June 9, 2019 – 9:47 AM

Reference: Einstein’s 1920 Book

Appendix II
Minkowski’s Four-Dimensional Space (“World”)

Please see Appendix 2 at the link above. This appendix is supplementary to Section XVII.

We can characterize the Lorentz transformation still more simply if we introduce the imaginary √(—1).ct in place of t, as time-variable.

According to the theory of relativity, the “time” enters into natural laws in the same form as the space coordinates. A four-dimensional continuum was described by Minkowski as the “world” instead of “space.” In this continuum, a “location” was defined as an “event in the world.”

This four-dimensional “world” bears a close similarity to the three-dimensional “space” of (Euclidean) analytical geometry. We can regard Minkowski’s “world” in a formal manner as a four-dimensional Euclidean space (with imaginary time co-ordinate); the Lorentz transformation corresponds to a “rotation” of the co-ordinate system in the four-dimensional “world.”

.

Comment

In the four-dimensional world continuum, the first three coordinates define the extents of the substance, and the fourth coordinated defines the consistency of the substance.

.

By vinaire | Comments (0)

Einstein 1920 (App I) Simple Derivation of the Lorentz Transformation

June 9, 2019 – 8:15 AM

Reference: Einstein’s 1920 Book

Appendix I
Simple Derivation of the Lorentz Transformation

Please see Appendix 1 at the link above. This appendix is supplementary to Section XI.

The Fig. 2 above provides the relative orientation of the co-ordinate systems K and K’. K is relatively at “rest” while K’ is moving at a velocity v.

The coordinates of K and K’ are different for the same event, but they are related by the fact that the velocity of light c is the same in both coordinate systems.

The coordinates for an event in K shall be related by constants to the corresponding coordinates in K’ because v is constant. This is true for motion in reverse direction for straight line motion.

We can relate the uniform velocity v to the constants involved in the correspondence of the coordinates of K and K’.

According to the principle of relativity the unit of lengths at rest in K or K’ will appear to be the same when viewed from the other system (K’ or K). From this we can determine the value of the constants involved in terms of v and c.

This gives us the following relationships between the coordinates of K and K’.

In this way we satisfy the postulate of the constancy of the velocity of light in vacuo for rays of light of arbitrary direction, both for the system K and for the system K’. We have thus derived the Lorentz transformation.

.

By vinaire | Comments (0)