Reference: Einstein’s 1920 Book
Appendix II
Minkowski’s Four-Dimensional Space (“World”)
Please see Appendix 2 at the link above. This appendix is supplementary to Section XVII.
We can characterize the Lorentz transformation still more simply if we introduce the imaginary √(—1).ct in place of t, as time-variable.
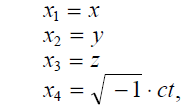
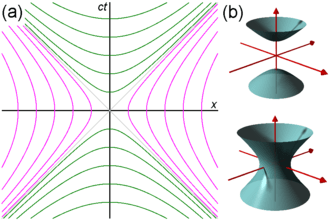
According to the theory of relativity, the “time” enters into natural laws in the same form as the space coordinates. A four-dimensional continuum was described by Minkowski as the “world” instead of “space.” In this continuum, a “location” was defined as an “event in the world.”
This four-dimensional “world” bears a close similarity to the three-dimensional “space” of (Euclidean) analytical geometry. We can regard Minkowski’s “world” in a formal manner as a four-dimensional Euclidean space (with imaginary time co-ordinate); the Lorentz transformation corresponds to a “rotation” of the co-ordinate system in the four-dimensional “world.”
.
Comment
In the four-dimensional world continuum, the first three coordinates define the extents of the substance, and the fourth coordinated defines the consistency of the substance.
.