Reference: Einstein’s 1920 Book
Section XXV (Part 2)
Gaussian Co-ordinates
Please see Section XXV at the link above.
.
Summary
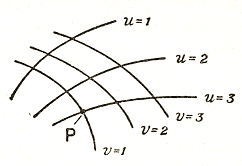
Gauss invented a method for the mathematical treatment of continua in general, in which “size-relations” (“distances” between neighbouring points) are defined. To every point of a continuum are assigned as many numbers (Gaussian co-ordinates) as the continuum has dimensions. This is done in such a way, that only one meaning can be attached to the assignment, and that numbers (Gaussian co-ordinates) which differ by an indefinitely small amount are assigned to adjacent points.
The Gaussian co-ordinate system is a logical generalization of the Cartesian co-ordinate system. It is also applicable to non-Euclidean continua, but only when, with respect to the defined “size” or “distance,” small parts of the continuum under consideration behave more nearly like a Euclidean system, the smaller the part of the continuum under our notice.
.
Final Comments
Mathematics serves as a tool to arrive at better understanding of what is being observed. It has its own postulates and very fine logic.
Mathematics helps derive relationships among variables. Calculations from such relationships are then verified against actual experiments and experience. The correctness of verification then validates the application of such mathematics to that situation. Any conclusions must not violate the sense of continuity, consistency and harmony.
.