Vinaire's Blog

Reference: Einstein’s 1920 Book

Section XXVII (Part 2)
The Space-Time Continuum of the General Theory of Relativity Is not a Euclidean Continuum

Please see Section XXVII at the link above.

.

Summary

The space time continuum of the special theory can be regarded as four-dimensional Cartesian co-ordinates if we consider the velocity of light to be constant. For a rotating body of reference, a gravitational field is present; and, therefore, the velocity of light will depend on the coordinates. We cannot consider four-dimensional Cartesian co-ordinates in the general theory of relativity.

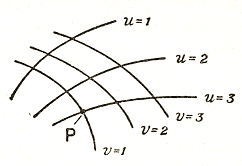
We refer the four-dimensional space-time continuum in an arbitrary manner to Gauss co-ordinates. In themselves these co-ordinates have no significance. A momentary existence of a material point at a location without duration will be represented by a single coordinate point. A permanent existence of a material point with motion shall then be represented by an infinitely large number of coordinate points as in a continuous line. Encounters among material points shall be represented by coincidences among coordinate points.

The motion of a material point relative to a body of reference shall be represented by encounters of that material point with particular points of the reference-body. This will take into account all kind of variations in both space and time in terms of flexibility, inertia or consistency.

All physical descriptions of space-time relationships can then be represented by coincidences among Gaussian coordinates of a body with a reference body. The Gaussian coordinates do not suffer the limitation of absolute rigidity of the Cartesian coordinates.

.

Final Comments

A body in uniform motion may not have acceleration, but it has a constant velocity. This constant velocity differs from body to body due to differences in their inherent structure. This inherent structure appears as the mass, inertia, rigidity or consistency of the body.

Light has near zero consistency and near infinite velocity; whereas, matter has near infinite consistency and extremely low range of velocities. By extrapolating between these data points, the special theory of relativity manages to come up with an approximate method to calculate the relative velocity in uniform motion for matter.

The general theory of relativity accounts for acceleration by relating instantaneous changes in consistency to changes in velocity throughout a continuum. Thus, it accounts for acceleration that manifests in the form of gravitational field.

.

Reference: Einstein’s 1920 Book

Section XXV (Part 2)
Gaussian Co-ordinates

Please see Section XXV at the link above.

.

Summary

Gauss invented a method for the mathematical treatment of continua in general, in which “size-relations” (“distances” between neighbouring points) are defined. To every point of a continuum are assigned as many numbers (Gaussian co-ordinates) as the continuum has dimensions. This is done in such a way, that only one meaning can be attached to the assignment, and that numbers (Gaussian co-ordinates) which differ by an indefinitely small amount are assigned to adjacent points.

The Gaussian co-ordinate system is a logical generalization of the Cartesian co-ordinate system. It is also applicable to non-Euclidean continua, but only when, with respect to the defined “size” or “distance,” small parts of the continuum under consideration behave more nearly like a Euclidean system, the smaller the part of the continuum under our notice.

.

Final Comments

Mathematics serves as a tool to arrive at better understanding of what is being observed. It has its own postulates and very fine logic.

Mathematics helps derive relationships among variables. Calculations from such relationships are then verified against actual experiments and experience. The correctness of verification then validates the application of such mathematics to that situation. Any conclusions must not violate the sense of continuity, consistency and harmony.

.

Reference: Einstein’s 1920 Book

Section XXIII (Part 2)
Behaviour of Clocks and Measuring Rods on a Rotating Body of Reference

Please see Section XXIII at the link above.

.

Summary

The physical interpretation of the space-time continuum in the context of the general theory of relativity may require some patience and power of abstraction. In a Galilean space-time continuum, only uniform motion is manifested. But in the general space-time continuum, inertia or consistency is also manifested due to curvilinear motion. This is taken as the effect of a gravitational field. The general law of gravitation would then be expected to explain not only the motion, but also the inertia/consistency of the stars.

In the given thought experiment, the reference point at the edge of the rotating disc will have much greater motion and flexibility than the reference point at the center of the disc. Therefore, measurements by clocks and rods will differ greatly at the two locations. As a result, the physical interpretation of the space-time continuum shall differ greatly in the gravitational field observed.

.

Final Comments

The space-time continuum in the gravitational field of a rotating body of reference shall have a varying sense of  inertia/consistency associated with different locations.

.